Languages
Back
Languages
Prime Factorization
> ... Math > Fractions > Prime Factorization

Introduction

In this lesson, you will learn the basic structure of prime factorization. A prime number can only be divided by one and itself.

These videos illustrate the lesson material below. Watching the videos is optional.

Identifying Prime Numbers

Learning how to find the prime factorization of a number is important when you start learning about fractions. It is especially important when reducing fractions. Here are some vocabulary words that will help you with this lesson:

  • Factor: The numbers in a multiplication operation. (For example: In \(3\times4=12\), 3 and 4 are the factors of 12.)
  • Product: The solution to multiplication.  (For example: In \(3\times4=12\), 12 is the product.)
  • Prime Number: Any number where the only factors are 1 and itself (for example: 11 is a prime number. There is no other number other than 1 and 11 you can divide it by that will give you a whole number).
The image shows the Multiplication Chart.

Figure 1

Using the multiplication chart above, consider the following numbers and learn how to determine whether a number is prime:

  1. One is not considered prime; it is just the number one. There are reasons for that which aren't necessary to learn now. Just know that number one is not considered prime.
  2. Two is \(1\times2\) and it’s also \(2\times1\), but those are the only instances where you see the number two on the multiplication chart. So, two is only the product of one and itself, which makes it a prime number.
    • Note: Number two is the only even number that is prime; all others are odd numbers. However, not every odd number is prime.
  3. Four is the multiple of \(1\times4\), \(4\times1\), and \(2\times2\). Four can’t be a prime number because it has other factors—1, 2, 4. Remember, factors are numbers that, when multiplied together, create a product.
  4. Seven is the product of \(1\times7\) and \(7\times1\). But again, those are the only two cases where three appears on the chart, which indicates that three is prime.

What are some other prime numbers on the chart? Figure 2 highlights the prime numbers in yellow up to number 139.

A chart that highlights the prime numbers.

Figure 2

Prime Factorization

The smallest numbers you can break a number down into are prime numbers because a prime number cannot be broken down any further.

Example 1
14 isn’t prime because it is the same as \(2\times7\).

This figure shows that 14 can be factored using 2 and 7.

Figure 3

The factorization is \(2\times7\). To factor a number, break it down by listing the factors underneath, creating a tree-like shape. Then evaluate the factors. Because the factors 2 and 7 are both prime, this is as far as you can factor 14. Therefore, 2 and 7 are the prime factors of 14.

Example 2
There are lots of ways you can get 40, such as \(8\times5=40\) and \(4\times10=40\). This means that 40 can be factored multiple ways. First, try using the factors 4 and 10.

This figure shows how 40 can be factored in multiple ways starting with 4 and 10, and under 4 are 2 and 2, while under 10 are 2 and 5.

Figure 4

4 is not prime, so you can break it down even further. \(2\times2=4\), and 2 is prime, so that’s as far as you can go with the 4. The other factor, 10, is not prime either. 10 can be broken down into \(2\times5=10\), and 2 and 5 are both prime.

The prime factorization of 40 is \(2\times2\times2\times5\), or you could even put this in exponential notation as \(2^{3}\times5\). Both of these formats convey the correct answer.

Now try using the factors of 8 and 5 because 40 can also be broken down into \(8\times5\). The figure below shows this factorization.

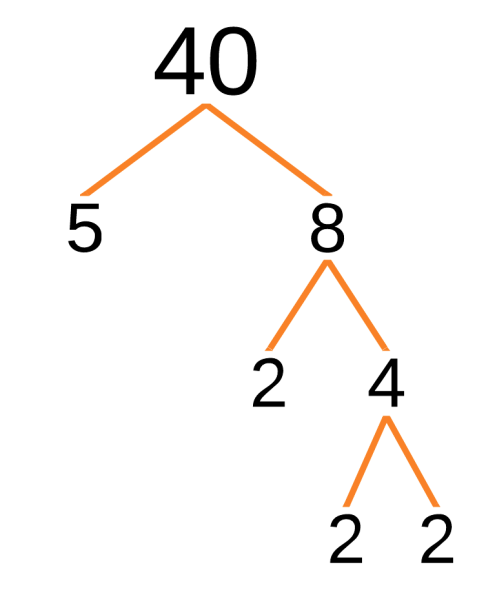
This figure shows that 40 can also be broken down using 5 and 8, 8 can be broken down using 2 and 4, while 4 can be broken down using 2 and 2.

Figure 5

Factoring it this way still got \(2\times2\times2\times5\) as the prime factors of 40.

Example 3
What is the prime factorization of 19? Look through the chart and see what multiples make up 19 before looking at Figure 6 below.

This figure shows numbers 9 and 1 make up 19.

Figure 6

Because 19 doesn’t have any multiples other than 1 and 19, that is where factorization stops. 19 is a prime number.

Example 4
210 has a factor of 2 because it is an even number. \(2\times105\). 105 has a prime factor of 5 because it ends with 5: \(5\times21\). 21 has two prime factors of 3 and 7. So the prime factorization of 210 is \(2\times5\times3\times7\).

The image shows 210 has prime factors of 2 and 105. 105 has two prime factors of 5 and 21, while number 21 has two prime factors of 3 and 7.

Figure 7

Once you know what prime numbers are, you learn that each number is made up of smaller prime numbers. Breaking a number down into the prime numbers that make it is called prime factorization. Every number has a prime factorization. For prime numbers, their only factors are themselves and 1.

Things to Remember


  • Prime numbers are numbers that can only be divided by one and itself.
  • Prime numbers are made up of odd numbers, except the number two. But remember that not every odd number is prime.
  • Factors are numbers that create a product.
  • Factoring out the number means you go all the way to the prime numbers. This can be done with any number you are given, even a prime number, although you won’t get very far.

Practice Problems

Find the prime factorization of the following numbers:
  1. 21 (
    Solution
    x
    Solution: \(21 = 3 \times 7\)
    Details:
    The number 21 is at the top of the image. Under 21 are two arrows pointing down and outward, one pointing to the right and one to the left. The arrow pointing to the left points down to the number 3. The arrow pointing down and to the right points to the number 7. There is a multiplication sign between the numbers 3 and 7 indicating that 3 times 7 is 21.
    \(3 \times 7 = 21\); and 3 and 7 are prime factors. The prime factorization of the number 21 is 3 and 7.
    )
  2. 13 (
    Solution
    x
    Solution: \(13 = 1 \times 13\)
    Details:
    The number 13 is at the top of the image. Under 13 are two arrows pointing down and outward, one pointing to the right and one to the left. The arrow pointing to the left points down to the number 1. The arrow pointing down and to the right points to the number 13. There is a multiplication sign between the numbers 1 and 13 indicating that 1 times 13 is 13.
    The definition of a prime number is any number where the only factors are 1 and itself.
    The only factors of 13 are 1 and itself, 13. The prime factorization of 13 is just 13.
    )
  3. 30 (
    Video Solution
    x
    Solution: \(30 = 2 \times 3 \times 5\)
    Details:

     | Transcript)
  4. 12 (
    Solution
    x
    Solution: \(12 = 2 \times 2 \times 3\)
    Details:
    First, find the factors of 12. There are a few ways to factor 12. It can be factored as either \(4 \times 3\) or \(6 \times 2\)
    This shows the first step in the prime factorization of 12. It starts with 12 at the top. Under the 12 are two arrows pointing down and outward in opposite directions. The arrow pointing down and out to the left points to a number 4. The arrow pointing down and out to the right points to a number 3. There is an x between the 4 and 3 indicating that 4 times 3 is 12.
    This displays a second version of the factorization of the number 12. It also starts with 12 at the top. Below this 12 is another set of downward pointing arrows. The arrow pointing down and to the left points to the number 6 and the arrow pointing down and to the right points to the number 2. There is an x between the 6 and the 2 indicating that 6 times 2 is 12.
    The numbers 3 and 2 are both prime, but 4 and 6 are not.
    Find the factors of 4 or 6. Notice how the prime factorization of 12 is \(2 \times 2 \times 3\) whether the starting factors were \(4 \times 3\) or \(6 \times 2\). The prime factorization is the same.
    This image is a continuation of the first version for the factorization of 12. Again it starts with 12 at the top with arrows pointing down to 4 on the left and 3 on the right. Below the 4 is another set of downward arrows. These arrows point to a 2 on the left and a two on the right. There is an x between the two twos meaning 2 times 2 is 4. The 2, 2, and 3 are all in red indicating they are all prime numbers.
    This is a continuation of the second version of the factorization of 12. Again, below the 12 is a set of downward pointing arrows. The arrow on the left points to a 6 and the arrow on the right points to a 2. Below the 6 is another set of downward pointing arrows. The arrow pointing down and to the left points to a 3 and the arrow pointing down and to the right is pointing to a 2. There is an x between the 3 and 2 indicating that 3 times 2 is 6. The numbers 3, 2, and 2 are all red because they are prime.
    )
  5. 54 (
    Solution
    x
    Solution: \(54 = 2 \times 3 \times 3 \times 3\)
    Details: 54 is an even number so you know it is divisible by 2.
    \(2 \times 27 = 54\)
    This shows the first step in the prime factorization of 54. It starts with 54 at the top. Under the 54 are two arrows pointing down and outward in opposite directions. The arrow pointing down and out to the left points to a number 2. The arrow pointing down and out to the right points to a number 27. There is an x between the 2 and 27 indicating that 2 times 27 is 54.
    The number 2 is prime, but 27 is not, so you must find the factors of 27.
    27 is divisible by 3:
    \(3 \times 9 = 27\)
    This image is a continuation of the first version for the factorization of 54. Again it starts with 54 at the top with arrows pointing down to a red 2 on the left and black 27 on the right. Below the 27 is another set of downward arrows. These arrows point to a red 3 on the left and a red 9 on the right. There is an x between the 3 and 9 meaning 3 times 9 is 27.
    The number 3 is a prime number, but 9 is not prime, so you must find the factors of 9.
    9 is also divisible by 3:
    \(3 \times 3 = 9\)
    This image is the third of three in the factorization of 54. Again it starts with 54 at the top with arrows pointing down to a red 2 on the left and black 27 on the right. Below the 27 is another set of downward arrows. These arrows point to a red 3 on the left and a black 9 on the right. There is an x between the 3 and 9 meaning 3 times 9 is 27. Under the 9 is a red 3 on the left and a red 3 on the right, with an x in between meaning 3 times 3 is 9. The red numbers indicate prime numbers.
    The number 3 is a prime number so there are actually two more 3’s in this prime factorization.
    Now look back and find all the prime numbers in the factorization of 54.
    This image is the same as the previous image, third of three in the factorization of 54. Again it starts with 54 at the top with arrows pointing down to a red 2 on the left and black 27 on the right. Below the 27 is another set of downward arrows. These arrows point to a red 3 on the left and a black 9 on the right. There is an x between the 3 and 9 meaning 3 times 9 is 27. Under the 9 is a red 3 on the left and a red 3 on the right, with an x in between meaning 3 times 3 is 9. The red numbers have a box around each one, indicating prime numbers.
    \(54 = 2 \times 3 \times 3 \times 3\)
    )
  6. 250 (
    Video Solution
    x
    Solution: \(250 = 2 \times 5 \times 5 \times 5\)
    Details:

     | Transcript)
Introduction to Fractions