Introduction
In this lesson, you will learn how to find the perimeter (outside measurement) of triangles.
This video illustrates the lesson material below. Watching the video is optional.
Perimeter of a Triangle
The perimeter of a triangle is found the same way as the perimeter of a rectangle. It is the sum of the length of all sides. In this course, you will be given the lengths of the sides of a triangle in order to find the perimeter. Finding the lengths of the sides is outside the scope of this course.
Here are some vocabulary words to review for this lesson:
- Triangle: a 3-sided shape.
- Equilateral Triangle: a triangle whose sides are all the same length.
- Perimeter of a triangle: sum of the length of all sides of the triangle.
When given the measurements of each side, add them together. The result will be the triangle’s perimeter. For a triangle with sides a, b, and c:
\begin{align*} Perimeter=a+b+c \end{align*}
Example 1
A triangle has sides that measure \(a =100\), \(b = 210\), and \(c =285\). Find the perimeter.
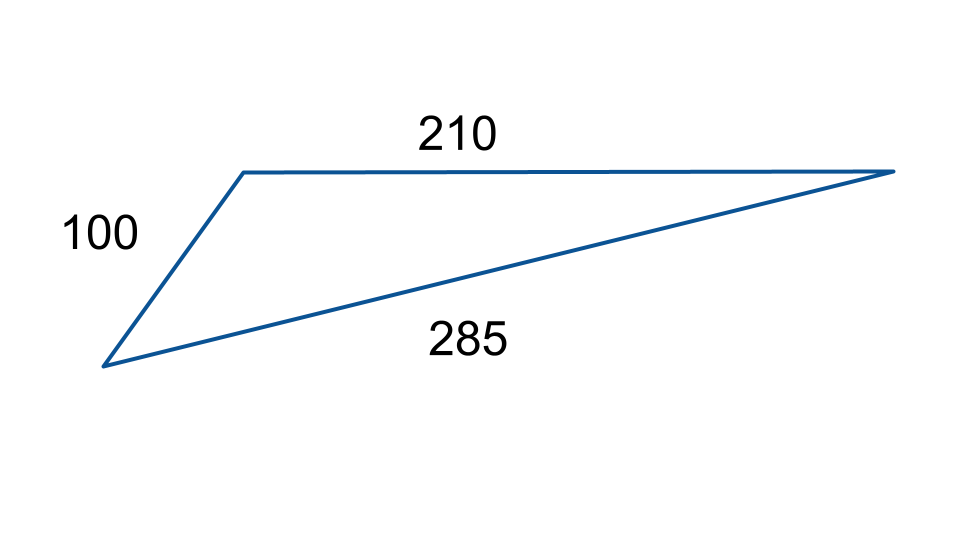
Figure 1
\begin{align*} Perimeter & =a+b+c &\color{navy}\small\text{Formula for perimeter of a triangle} \\\\ P&=100+210+285 &\color{navy}\small\text{Substitute given terms}\\\\ P&=595 &\color{navy}\small\text{Add} \end{align*}
The perimeter of the triangle is 595 units.
Equilateral Triangles
Equilateral triangles are slightly different from ordinary triangles. Their sides are all the same length. For these, the formula is:
\begin{align*} Perimeter&=a+a+a\\\\ Perimeter&=3a \end{align*}
Adding a three times and multiplying a by 3 will have the same result.
Example 2
An equilateral triangle has sides that are 8 units. Find the perimeter.
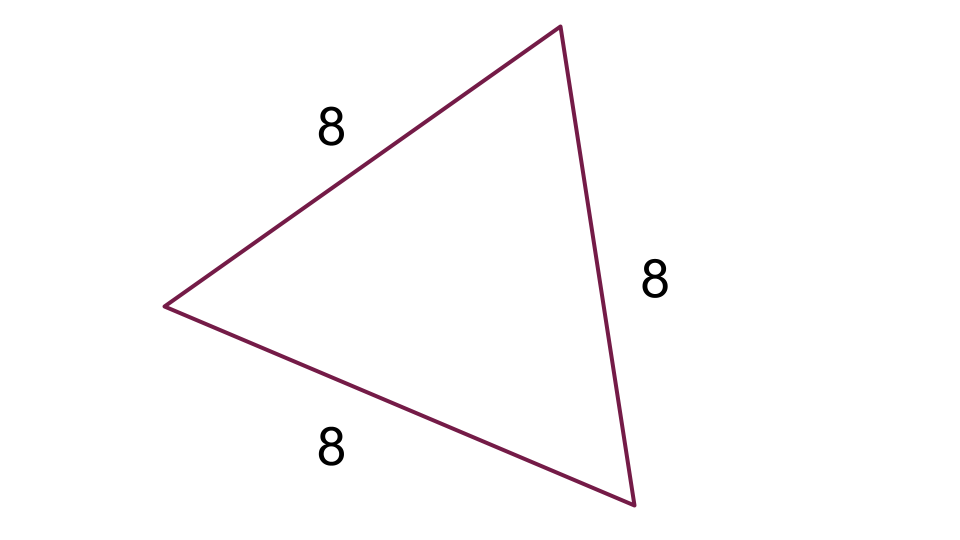
Figure 2
\begin{align*}Perimeter &= a + a + a &\color{navy}\small\text{Formula for an equilateral triangle}\\\\P &= 8 + 8 + 8 &\color{navy}\small\text{Substitute given terms}\\\\ P& = 24\;units &\color{navy}\small\text{Add}\end{align*}
You can check the answer by multiplying 8 by 3 since the sides are equivalent.
\begin{align*}Perimeter &= 3a &\color{navy}\small\text{Formula for an equilateral triangle}\\\\ P &= 3\times8&\color{navy}\small\text{Substitute given terms}\\\\ P&=24\;units &\color{navy}\small\text{Multiply}\\\ \end{align*}
As you can see, you can use either method to find the perimeter of an equilateral triangle which is equal to 24 units.
Example 3
A triangle has sides that measure: 29, 31, and 15. Find the perimeter.
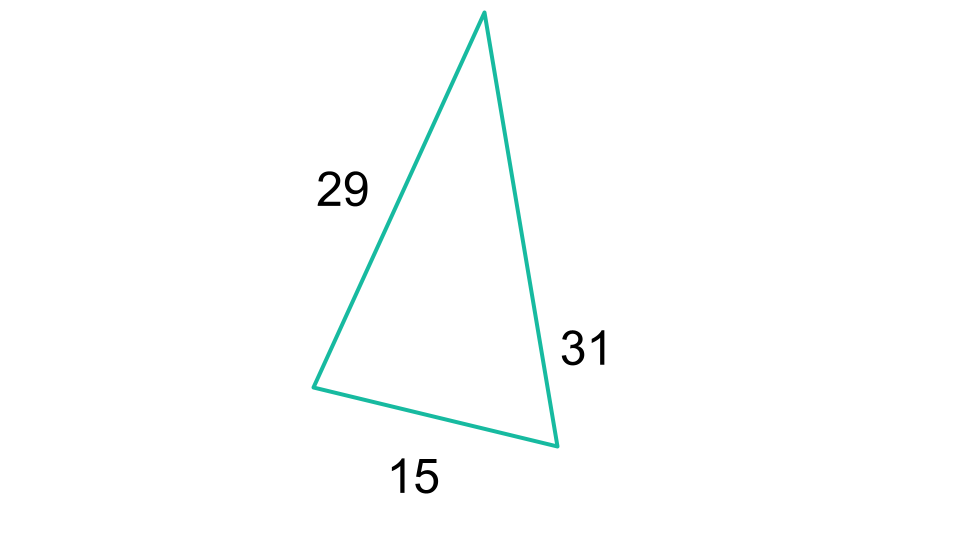
Figure 3
This is not an equilateral triangle because its sides are different lengths. To find the perimeter, add all the sides together.
\begin{align*}Perimeter &= a + b + c &\color{navy}\small\text{Formula for perimeter of any triangle}\\\\P &= 29 + 31+ 15 &\color{navy}\small\text{Substitute given terms}\\\\P& = 75 &\color{navy}\small\text{Add}\end{align*}
The perimeter of the triangle is 75 units.
Things to Remember
- The formula for the perimeter of a triangle is: \( P=a+b+c\)
- An equilateral triangle can be identified when all sides have the same length.
- You can find the perimeter of an equilateral triangle by this formula \(P=3a\), where a represents one side of the triangle.
Practice Problems
- Find the perimeter of a triangle with sides a, b, and c, where a = 14, b = 20, and c = 8. (
- Find the perimeter of a triangle with sides a, b, and c, where a=12.5, b=13.8, and c=16.3. Round your answer to the nearest tenth. (
- Oliver is building a garden that is in the shape of a triangle with sides of length 9 m, 12 m, and 5 m. If Oliver wants to build a fence around the perimeter of his garden, how many meters of fencing does he need to buy? (
Details:
Oliver wants to put up a fence around his garden so he needs to find out how many meters of fencing he needs to go around the entire garden.
To find out how much fencing he needs, he will have to find the perimeter of his garden. Since the garden is shaped like a triangle, the perimeter is the sum of the lengths of all three sides.
\(12 + 5 + 9 = 26\)
Oliver will need to purchase 26 meters of fencing. - Gabriel rides his bike every morning and follows a path that forms a triangle with distances of 8.4km, 12.5km, and 9.2km. When Gabriel finishes his bike ride, how far has he ridden? Round to the nearest tenth. (
- An equilateral triangle has sides of length 6 m. Find the perimeter of this equilateral triangle. (
Details:
The triangle is an equilateral triangle. That means that all three sides have the same length. In this case, all three sides are 6 m long.
To find the perimeter of an equilateral triangle, you need to add all three side lengths together.
\(6 + 6 + 6 = 18\)
The perimeter of the triangle is 18 meters long. - A triangle has sides with lengths a, b, and c. The length of side a is 15 inches, and side b is two more inches than side a. If the perimeter of the triangle is equal to 40 inches, what is the length of side c? (
- A triangular slice of pizza has a perimeter of 45 centimeters (cm). One side of the pizza slice is 18 cm with an adjacent side that is half the length of the first side. What is the length of the third side? (