Introduction

In this lesson, you will review how to find the x- and y-intercepts of a line.

This video illustrates the lesson material below. Watching the video is optional.

• X and Y Intercepts of a Line (02:48 mins) | Transcript

X- and Y-Intercepts

Intercepts are an important part of graphs. They indicate a lot about data. For example, y-intercepts often give a starting amount. Here are some vocabulary words to help you with this lesson:

• x-intercept: where the graph crosses the x-axis, and where \(y = 0\)
• y-intercept: where the graph crosses the y-axis, and where \(x = 0\)

The x-intercept is anywhere that the line crosses the x-axis. The x-axis is also known as the horizontal axis. The y-intercept is anywhere that the line crosses the y-axis.

Figure 1

At the y-intercept point, \(x=0\). Similarly, at the point at which the line crosses the x-axis, \(y=0\). At the point where the line crosses the x-axis, y will always be 0. The value of x will change depending on the line, but any time the line crosses the x-axis, \(y=0\).

Any time the line crosses the y-axis, x has to be 0. The value of y may be different, but the y-axis will be where it crosses.

When you know this information, you still need to estimate the value of x for the x-intercept and the value of y for the y-intercept.

Example 1

Estimate the x-intercept and y-intercept of the line in Figure 2.

Figure 2

If you look at the x-intercept, you can estimate it at 1.5. The estimated x-intercept is written as: \((1.5, 0)\).

The y-intercept is approximately at 3. The estimated y-intercept is written as \((0, 3)\).

Things to Remember

• At the x-intercept point, \(y=0\).
• At the y-intercept point, \(x=0\).

Practice Problems

 

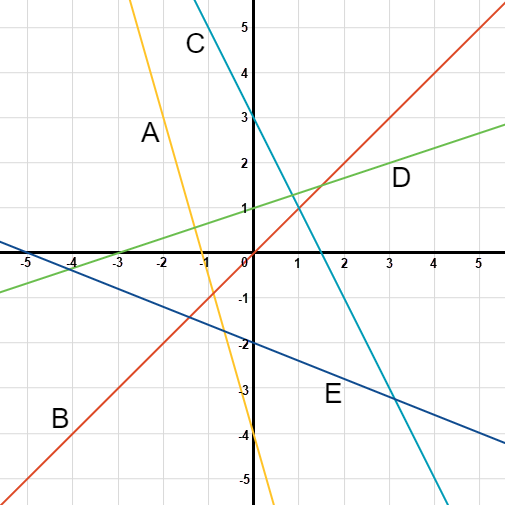
1. What is the y-intercept of line A? (
   Solution

   x

   Solution:
   Y-intercept: \((0, -4)\)
   )
2. What is the x-intercept of line B? (
   Solution

   x

   Solution:
   X-intercept: \((0, 0)\)
   )
3. What is the y-intercept of line B? (
   Solution

   x

   Solution:
   Y-intercept: \((0, 0)\)
   )
4. What are the x-intercept and y-intercept of line C? (
   Solution

   x

   Solution:
   X-intercept: \((1.5, 0)\)
   Y-intercept: \((0, 3)\)
   
   Details:
   To find the x-intercept, look for the point where the line crosses the x-axis. The line crosses the x-axis where the x-value is approximately \(1.5\). The y-value is always \(0\) for every point on the x-axis so the x-intercept is \((1.5, 0)\).
   
   To find the y-intercept, look for the point where the line crosses the y-axis. The line crosses the y-axis where the y-value is \(3\). The x-value is always \(0\) for every point on the y-axis so the y-intercept is \((0, 3)\).
    
   )
5. What are the x-intercept and y-intercept of line D? (
   Solution

   x

   Solution:
   X-intercept: \((-3, 0)\)
   Y-intercept: \((0, 1)\)
   
   Details:
   To find the x-intercept, look for the point where the line crosses the x-axis. The line crosses the x-axis where the x-value is approximately \(-3\). The y-value is always 0 for every point on the x-axis so the x-intercept is \((-3,0)\).
   
   To find the y-intercept, look for the point where the line crosses the y-axis. The line crosses the y-axis where the y-value is \(1\). The x-value is always 0 for every point on the y-axis so the y-intercept is \((0, 1)\).
    
   )
6. What are the x-intercept and y-intercept of line E? (
   Solution

   x

   Solution:
   X-intercept: \((-5, 0)\)
   Y-intercept: \((0, -2)\)
   )