Introdução

Nesta lição, você aprenderá os passos da subtração. Ao fazer subtração com números grandes demais para serem feitos de cabeça, há passos que você pode seguir que te ajudam a fazer a subtração corretamente.

Esses vídeos ilustram o material da lição abaixo. Assistir aos vídeos é opcional. No vídeo chamado “Passos da Subtração”, apenas os passos 1 a 3 são relevantes para esta lição.

• Etapas da Subtração | Transcrição
• Reagrupamento | Transcrição

Passos da Subtração

1. Empilhe por valor posicional, com o maior número no topo.
2. Agrupe-os novamente quando necessário. Isso é necessário quando o número de cima é menor que o número de baixo em uma coluna de valor posicional.
3. Subtraia em colunas por valor posicional, começando pela direita e indo para a esquerda.

Veja aqui alguns exemplos para ilustrar esses passos.

Exemplo 1

\(9-3\)

O primeiro passo te instrui a empilhar por valor posicional, com o maior número no topo. Coloque o 9 em cima do 3, já que 9 é o número maior. Há apenas um dígito em cada número, então ambos serão colocados na coluna das unidades. Sua equação deve ficar mais ou menos assim:

Figura 1

Agora que você configurou o problema, você pode subtrair. A resposta é 6.

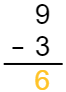
Figura 2

Exemplo 2

\( 56-42\)

Organize de acordo com o tamanho do número e o valor posicional. O número 56 é o maior, então deve estar em cima de 42. Há dois dígitos em cada número, então você alinhará o 6 e o 2 na coluna das unidades e alinhará o 5 e o 6 na coluna das dezenas.

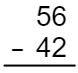
Figura 3

Subtraia as colunas por valor posicional, começando pela direita e indo para a esquerda: \(6-2=4\) e \(5-4=1\). A resposta final é 14.

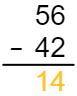
Figura 4

Reagrupamento

O reagrupamento é o segundo passo no processo de subtração. Nem sempre é necessário, como nos exemplos acima, mas é um passo importante de se entender.

Exemplo 3

\(25-7\)

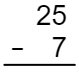
Figura 5

Neste exemplo, o primeiro passo já foi realizado, alinhando os números por valor posicional (unidades em cima de unidades), com o maior número em cima. Você pode considerar adicionar um zero na frente do 7, só para ver como os números se alinham.

Para o segundo passo, observe que 5 é maior que 7. Para facilitar a solução desta equação, você precisa reagrupar, tomando emprestado da coluna das dezenas.

Quando você pega emprestado de uma coluna, você não apenas soma um ao número original. Você soma o valor total do que você toma emprestado. Como você está pegando emprestado da coluna das dezenas, um 10 deve ser somado à coluna das unidades. Você fará algumas adições simples para somar os 10 emprestados aos 5. Isso lhe dá 15 na coluna das unidades (consulte a Figura 6).

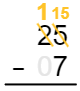
Figura 6

Agora você pode resolver esta equação. Comece pela direita (na coluna das unidades) e vá para a esquerda.

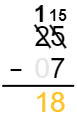
Figura 7

A resposta final é: \(25-7=18\).

Exemplo 4

\(452-273\)

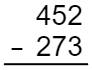
Figura 8

Os números já estão organizados conforme as instruções do passo um. Agora, determine se o problema precisa ser reagrupado. Observe na coluna das unidades que 2 é menor que 3, e que na coluna das dezenas 5 é menor que 7. Ambas as colunas precisarão pegar emprestado da coluna à sua esquerda (ver Figura 9).

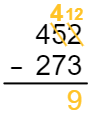
Figura 9

Como sempre, comece pela coluna das unidades. Assim como no primeiro exemplo, some 10 ao 2 na coluna das unidades, resultando em 12. Consequentemente, isso transformará o 5 na coluna das dezenas em um 4. Observe que você não alterou o número; você está apenas reorganizando onde eles estão de acordo com o valor posicional.

Em seguida, faça para a coluna das dezenas o mesmo que você fez para a coluna das unidades. Pegue emprestado do número à esquerda. Neste caso, isso significa pegar emprestado da coluna das centenas. Como você está pegando emprestado da coluna das centenas, você tem dez grupos de 10 somados à nossa coluna das dezenas. Faça uma soma simples para somar o grupo emprestado de dezenas às 4 dezenas originais. Isso lhe dá 14 dezenas (Figura 10).

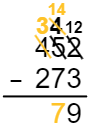
Figura 10

Passe para a próxima coluna. A subtração \(3-2\) funciona, então você simplesmente resolverá o resto da equação. Portanto, \(452 - 273 = 179\).

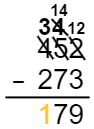
Figura 11

Lembre-se

1. Os passos da subtração:

   1. Organize os números de acordo com o tamanho e o valor posicional.
   2. Reagrupe conforme necessário.
   3. Subtraia os valores posicionais, da direita para a esquerda.
2. Ao pegar emprestado de uma coluna, você não soma apenas um ao número original. Você soma o valor total do que você toma emprestado.

1. \(64 - 32 = ?\) (
   Solução

   x

   Solução: 32
   Detalhes:
   Usando o valor posicional para subtrair, coloque o 6 na casa das dezenas e o 4 na casa das unidades.
   
   
   
   Em seguida, coloque o 3 na casa das dezenas e o 2 na casa das unidades.
   
   
   
   
   Subtraia os números na casa das unidades.
   \(4 − 2 = 2\)
   
   
   
   
   Por fim, subtraia os números na casa das dezenas.
   \(6 − 3 = 3\)
   
   
   
   
   
   A resposta é: \(64 − 32 = 32\)
   
   
   )
2. \(357 - 34 = ?\) (
   Solução

   x

   
   
   Solução: 323
   Detalhes:
   Use o valor posicional para subtrair. Coloque o 3 na casa das centenas, o 5 na casa das dezenas e o 7 na casa das unidades.
   
   
   
   Agora, coloque o 3 na casa das dezenas e o 4 na casa das unidades.
   
   
   
   
   Subtraia os números na coluna das unidades. \(7 − 4 = 3\)
   
   
   
   
   Subtraia os números na coluna das dezenas. \(5 − 3 = 2\)
   
   
   
   
   
   
   
   
   Subtraia os números na coluna das centenas. Como o 3 é o único número nesta coluna, a resposta é 3. Ou em outras palavras, 3 menos 0 é 3.
   
   
   
   
   A resposta para \(357 − 34\) é \(323\).
   )
3. \(963 - 69 = ?\) (
   Solução

   x

   Solução: 894
   )
4. \(884 - 500 = ?\) (
   Solução

   x

   Solução: 384
   )
5. \(800 - 263 = ?\) (
   Video Solução

   x

   Solução: 537
   Detalhes:
   

   
   
   | Transcrição)
6. \(577 - 284 = ?\) (
   Solução

   x

   Solução: 293
   )
7. \(954 - 597 = ?\) (
   Video Solução

   x

   Solução: 357
   Detalhes:
   

   
   
   | Transcrição)